sábado, 11 de octubre de 2014

Tridimensional

De Wikipedia, la enciclopedia libre

Saltar a: navegación, búsqueda

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Este aviso fue puesto el 28 de septiembre de 2012.
Puedes añadirlas o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Tridimensional}} ~~~~

«3D» redirige aquí. Para otras acepciones, véase 3D (desambiguación).

Esquema elemental de posicionamiento espacial, consistente en un marco de referencia respecto a un origen dado.

En física, geometría y análisis matemático, un objeto o ente es tridimensional si tiene tres dimensiones. Es decir cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Por ejemplo, anchura, longitud y profundidad.
El espacio a nuestro alrededor es tridimensional a simple vista, pero en realidad hay más dimensiones, por lo que también puede ser considerado un espacio tetra-dimensional si incluimos el tiempo como cuarta dimensión. La teoría de Kaluza-Klein original postulaba un espacio-tiempo de cinco dimensiones , la teoría de cuerdas retoma esa idea y postula según diferentes versiones que el espacio físico podría tener 9 o 10 dimensiones.

Índice

[ocultar]

Espacio físico tridimensional[editar]

Tres planos ortogonales en el espacio.

En un espacio euclídeo convencional un objeto físico finito está contenido dentro de un ortoedro mínimo, cuyas dimensiones se llaman ancho, largo y profundidad o altura. El espacio físico a nuestro alrededor es tridimensional a simple vista. Sin embargo, cuando se consideran fenómenos físicos como la gravedad, la teoría de la relatividad nos lleva a que el universo es un ente tetra-dimensional que incluye tanto dimensiones espaciales como el tiempo como otra dimensión. Diferentes observadores percibirán diferentes "secciones espaciales" de este espacio-tiempo por lo que el espacio físico es algo más complejo que un espacio euclídeo tridimiensional.
En las teorías actuales no existe una razón clara para que el número de dimensiones espaciales sean tres. Aunque existen ciertas instuiciónes sobre ello: Ehrenfest señaló que en cuatro o más dimensiones las órbitas planetarias cerradas, por ejemplo, no serían estables (y por ende, parece difícil que en un universo así existiera vida inteligente preguntándose por la tridimensionalidad espacial del universo). También se sabe que existe una conexión entre la intensidad de un campo de fuerzas estático con simetría esférica que se extiende sobre un espacio de d dimensiones y que satisface el teorema de Gauss y la dimensión del espacio (d), un campo gravitatorio, electrostático o de otro tipo que cumpla con dichas condiciones para grandes distancias debe tener una variación de la forma:

$\phi =k_\phi \frac{f}{r^{d-1}} \qquad d \ge 3$

Donde:

\phi\,

es la intensidad del campo.

k_\phi\,

es una constante de proporcionalidad (

k_\phi=-G\,

para el campo gravitatorio).

f\,

es una magnitud extensiva que mida la capacidad de fuente para provocar el campo, para un campo gravitatorio coincide con la masa y para uno eléctrico con la carga.

r\,

es la distancia al "centro" o fuente que crea el campo.

d\,

es la dimensión del espacio.

Si la geometría del espacio d-dimensional no es euclídea entonces la expresión anterior debe corregirse según la curvatura.
Por otra, teorías físicas de tipo Kaluza-Klein como las diferentes versiones de la teoría de cuerdas postula que existe un número adicional de dimensiones compactificadas, que sólo serían observables en experimentos con partículas altamente energéticas. En estas teorías algunas de las interacciones fundamentales pueden ser explicadas de manera sencilla postulando dimensiones adicionales de un modo similar a como la relatividad general explica la gravedad. De hecho la propuesta original de Theodor Kaluza explicaba de manera unificada el electromagnetismo y la gravedad postulando un universo de 5 dimensiones con una dimensión compactificada.

Ejemplos de formas tridimensionales[editar]

Forma tridimensional de una campana de Gauss.

En geometría son tridimensionales las siguientes figuras geométricas:

Poliedros de caras planas:
- Pirámides
- Cubo
- Prismas
Superficies curvas:
- Cilindro
- Conos
- Esfera o 3-esfera

Ya que todas ellas pueden ser embebidas en un espacio euclídeo de tres dimensiones. Sin embargo, hay que señalar que técnicamente la esfera, el cono o el cilindro son variedades bidimensionales (solo la cáscara) ya que los puntos interiores a ellos no son estrictamente parte de los mismos. Sólo por un abuso de lenguaje o extensión del mismo informalmente se habla de esferas, cilindros o conos incluyendo el interior de los mismos.
Por otra parte existe la hiperesfera tridimensional (3-variedad) pero no es la cáscara de una bola sino la compactificación de

\mathbb{R}^3

con un punto, así como la 2-esfera es para el plano euclídeo

\mathbb{R}^2

Sistemas tridimensionales en ciencias naturales[editar]

En química, se habla de sistemas tridimensionales cuando el enlace químico es igualmente intenso en las tres direcciones del espacio (por ejemplo, en el diamante). En magnetismo, se dice que el ordenamiento magnético sólo es posible si el acoplamiento magnético es tridimensional (se extiende en las tres direcciones del espacio). En matemáticas el sistema tridimensional se representa en el plano cartesiano con los ejes X, Y y Z. Por lo general en estas representaciones se manejan las formas geométricas de tres dimensiones como los cubos o las esferas en dos dimensiones utilizando perspectivas.

Simulación 3D[editar]

Hoy en día es posible la simulación mediante cálculos basados en la proyección de entornos tridimensionales sobre pantallas bidimensionales, como monitores o televisores. Estos cálculos requieren de una gran carga de proceso por lo que algunas computadoras y videoconsolas disponen de cierto grado de aceleración gráfica 3D gracias a dispositivos desarrollados para tal fin. Las computadoras disponen de las llamadas tarjetas gráficas con aceleración 3D. Estos dispositivos están formados por uno o varios procesadores (unidad de procesamiento gráfico) diseñados especialmente para acelerar los cálculos que suponen reproducir imágenes tridimensionales sobre una pantalla bidimensional y de esta forma liberar de carga de proceso a la unidad central de procesamiento de la computadora.

Véase

Tridimensional

De Wikipedia, la enciclopedia libre

Saltar a: navegación, búsqueda

«3D» redirige aquí. Para otras acepciones, véase 3D (desambiguación).

Esquema elemental de posicionamiento espacial, consistente en un marco de referencia respecto a un origen dado.

Índice

[ocultar]

Espacio físico tridimensional[editar]

Tres planos ortogonales en el espacio.

$\phi =k_\phi \frac{f}{r^{d-1}} \qquad d \ge 3$

Donde:

\phi\,

es la intensidad del campo.

k_\phi\,

es una constante de proporcionalidad (

k_\phi=-G\,

para el campo gravitatorio).

f\,

es una magnitud extensiva que mida la capacidad de fuente para provocar el campo, para un campo gravitatorio coincide con la masa y para uno eléctrico con la carga.

r\,

es la distancia al "centro" o fuente que crea el campo.

d\,

es la dimensión del espacio.

Ejemplos de formas tridimensionales[editar]

Forma tridimensional de una campana de Gauss.

En geometría son tridimensionales las siguientes figuras geométricas:

Poliedros de caras planas:
- Pirámides
- Cubo
- Prismas
Superficies curvas:
- Cilindro
- Conos
- Esfera o 3-esfera

\mathbb{R}^3

con un punto, así como la 2-esfera es para el plano euclídeo

\mathbb{R}^2

Sistemas tridimensionales en ciencias naturales[editar]

Simulación 3D[editar]

Véase

Deslizamiento (ciencia de materiales) Saltar a: navegación, búsqueda Modelo esquemático del mecanismo de deslizamiento En ciencia de materiales, deslizamiento es el proceso por el cual se produce deformación plástica por el movimiento de dislocaciones. Debido a una fuerza externa, partes de la red cristalina se deslizan respecto a otras, resultando en un cambio en la geometría del material. Dependiendo del tipo de red, diferentes sistemas de deslizamiento están presentes en el material. Más específicamente, el deslizamiento ocurre entre los planos que tienen el menor vector de Burgers, con una gran densidad atómica y separación interplanar. La imagen a la derecha muestra esquemáticamente el mecanismo de deslizamiento. Índice [ocultar] 1 Sistemas de deslizamiento 1.1 Estructura cúbica centrada en las caras (FCC) 1.2 Estructura cúbica centrada en el cuerpo (BCC) 1.3 Empaquetamiento hexagonal compacto (HCP) 2 Véase también 3 Referencias 4 Enlaces externos Sistemas de deslizamiento[editar] Un sistema de deslizamiento está definido por la combinación de un plano que se desliza y la dirección en que se da su desplazamiento. Estructura cúbica centrada en las caras (FCC)[editar] Celda unidad de un material FCC Configuración de red del plano de deslizamiento con empaquetamiento compacto en un material FCC. La flecha representa el vector de Burgers en este sistema de desplazamiento de dislocaciones. El deslizamiento en cristales cúbicos con centro en las caras ocurre en el plano de empaquetamiento compacto, el cual es del tipo {111} y se da en la dirección <110>. En el diagrama, el plano específico y su dirección de deslizamiento son (111) y [110] respectivamente. Dadas las permutaciones de los tipos de planos de deslizamiento y los tipos de dirección, los cristales CCC tienen 12 sistemas de deslizamiento. En la red FCC, la norma del vector de Burgers, b, que coincide con la mínima distancia entre dos puntos de la red, puede ser calculada usando la siguiente ecuación:1 |b|= \frac {a}{2}|<110>|= \frac{a}{\sqrt 2}1 Donde a es el parámetro de la celda unitaria. Estructura cúbica centrada en el cuerpo (BCC)[editar] Celda unidad de un material BCC Configuración de red del plano de deslizamiento en un material cúbico con centro en el cuerpo. La flecha representa el vector de Burgers en este sistema de desplazamiento de dislocaciones. El deslizamiento en cristales BCC ocurre también en el plano de menor vector de Burgers; sin embargo, a diferencia de en los FCC, no hay auténticos planos de empaquetamiento compacto en las estructuras BCC. Por consiguiente, un sistema de deslizamiento en BCC requiere calor para activarse. Algunos materiales BCC (α-Fe por ejemplo) pueden contener hasta 48 sistemas de deslizamiento. Existen seis planos de deslizamiento del tipo {110}, cada uno con direcciones <111> (12 sistemas). Además, hay 24 planos {123} y 12 planos {112}, cada uno con una dirección <111> (36 sistemas, haciendo un total de 48) que, aunque no tienen exactamente la misma energía de activación que los planos {110}, esta es tan cercana que se pueden aproximar como equivalentes para todos los propósitos prácticos. En el diagrama de la derecha, el plano de deslizamiento específico y su dirección son (110) y [111], respectivamente.1 Los metales elementales que se encuentran en la estructura BCC incluyen al litio, sodio, potasio, vanadio, cromo, manganeso, hierro, rubidio, niobio, molibdeno, cesio, bario, tantalio, tungsteno, radio y europio. Entre los materiales compuestos con estructura cristalina BCC se encuentran los haluros de cesio, a excepción del CsF. Empaquetamiento hexagonal compacto (HCP)[editar] El deslizamiento en estos metales es mucho más limitado que en las estructuras BCC y FCC. Esto ocurre porque existen poquísimos sistemas de deslizamiento activos en estas estructuras. La consecuencia de esto es que el metal es generalmente frágil y quebradizo. Los metales cadmio, cinc, magnesio, titanio y berilio tienen un plano de deslizamiento en {0001} y una dirección de <1120>. Esto define un total de 3 sistemas de deslizamiento según la orientación. No obstante, otras combinaciones son posibles.2 Véase también

homotecia

Homotecia Homotecia con centro O y λ>1. Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. En general una homotecia de razón (λ) diferente de 1 deja un único punto fijo, llamado centro. Índice [ocultar] 1 Definición 1.1 Propiedades 2 Homotecias en el plano real 3 Ejes de homotecia 4 Referencias 4.1 Bibliografía Definición[editar] Esquema de operación de una homotecia, en el plano euclídeo. Sea E un espacio vectorial sobre un cuerpo \scriptstyle \mathbb{K}. Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada \scriptstyle h_{C, k} envía un punto M del espacio vectorial sobre el punto M' tal que: (1a)M'- C = k(M-C)\, La ecuación anterior puede escribirse también como una transformación afín de la forma: (1b)M' = kM + (1-k)C \, La anterior relación puede escribirse vectorialmente en el plano como: \begin{bmatrix} m'_x \\ m'_y\\ 1 \end{bmatrix} = \begin{bmatrix} k & 0 & (1-k)c_x \\ 0 & k & (1-k)c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} m_x \\ m_y\\ 1 \end{bmatrix} Donde: M' = (m'_x, m'_y)\,, M = (m_x, m_y)\, y C = (c_x, c_y)\,. En tres o más dimensiones la fórmula anterior se generaliza trivialmente. Cuando el cuerpo de escalares son los Reales, una homotecia de centro el punto C y razón el número real k ≠ 0, es una transformación geométrica que hace corresponder a cada punto P otro punto P′ tal que (el vector es igual al resultado de multiplicar el vector por el número k). Si k es positivo, P′ está en la semirrecta de origen C que pasa por P. Propiedades[editar] La homotecia es una transformación afín, composición de una transformación lineal y una traslación, y por consiguiente conserva: el alineamiento: las imágenes de puntos alineados son alineados: (A,B,C) y (A', B', C') en la figura el centro de un segmento, y más generalmente el baricentro: la imagen del baricentro es el baricentro de las imágenes. En la figura, B es el centro de [A;C] y por lo tanto B' es el de [A';C'] La imagen de línea es otra línea paralela a la original. el paralelismo: dos líneas paralelas tienen imágenes paralelas. En la figura (B'E') // (C'D') porque (BE) //(CD). Si k ≠ 1, el centro de la homotecia es el único punto fijo (k = 1 corresponde a la identidad de E: todos los puntos son fijos). k = - 1 corresponde a una simetría de centro C. Si k ≠ 0, \scriptstyle h_{C, k} admite como trasformación recíproca \scriptstyle h_{C, 1/k} (cuando k = 0, no es biyectiva). Al componer dos homotecias del mismo centro se obtiene otra homotecia con este centro, cuya razón es el producto de las razones de las homotecias iniciales: \scriptstyle h_{C, k} o \scriptstyle h_{C, k'} = \scriptstyle h_{C, k\cdot k'}. Al componer homotecias de centros distintos, de razones k y k', se obtiene una homotecia de razón k·k' cuando k·k'≠1, y una traslación si k·k'=1. El conjunto de las homotecias (con k≠0) y las translaciones forman un grupo. Cuando el cuerpo de escalares son los Reales, se cumple que: todas las longitudes son multiplicadas por |k|, el valor absoluto de la razón. el cociente de longitudes es conservado: A'C'/B'E' = AC/BE en la figura los ángulos orientados son conservados, en particular los ángulos rectos. Es obvio en la figura. Más aún: k = - 1 corresponde a la simetría de centro C que es la rotación alrededor de C de ángulo π radianes (180º). |k| > 1 implica una ampliación de la figura. |k| < 1 implica una reducción. k < 0, la homotecia se puede expresar como la composición de una simetría con una homotecia de razón |k|, ambas de igual centro. Que la homotecia original. Homotecias en el plano real[editar] Homotecia En esta sección, los escalares serán números reales. Una homotecia generalizada en el plano es una transformación del plano en sí mismo en donde una recta y su homóloga son paralelas. De esta definición, se sigue fácilmente que las homotecias conservan ángulos, es decir son transformaciones conformes del plano, que el conjunto de homotecias forman un 'grupo' y que las traslaciones son casos particulares de las homotecias. Consideremos la homotecia en la cual la recta OA se transforma en la recta O'B, siendo O' el homólogo de O y B el homólogo de A. Necesariamente, las rectas OO' y AB son invariantes en esta homotecia y el punto H1, centro de la homotecia, es invariante. En esta homotecia la circunferencia de centro O y radio OA se transforma en la circunferencia de centro O' y de radio O'B y la razón de la homotecia es la razón (positiva) de los segmentos O'B y OA. Si por el contrario, el punto A se transforma en B' entonces la recta AB' es invariante y es el punto H2 el centro de homotecia. En este caso, la razón de la homotecia es negativa. Ejes de homotecia[editar] Homothethyaxes.svg Dadas dos circunferencias, éstas siempre se pueden considerar como homotéticas una de la otra. En la figura, la circunferencia S2 puede considerarse homotética de s1 bien es en la homotecia de razón positiva, con centro en P1, o de razón negativa, con centro de homotecia en N1. Consideremos las homotecias, una con centro en P1 en la cual la circunferencia S2 es homotética de la circunferencia s1, y la homotecia de centro P3 en la que la circunferencia s3 es homotética a la circunferencia s2. La composición de estas dos homotecias es la homotecia de centro en P2 que transforma la circunferencia s1 en la circunferencia s3. Es por esta razón que los centros de homotecia positivos, P1, P2 y P3 están alineados. En general, dadas tres circunferencias existen seis centros de homotecia, alineados tres a tres sobre cuatro rectas. Estas rectas son las llamadas ejes de homotecia de las tres circunferencias dada

Movimiento de rotación (Redirigido desde «Rotacion») Commons-emblem-question book orange.svg Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Este aviso fue puesto el 18 de agosto de 2013. Puedes añadirlas o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Movimiento de rotación}} ~~~~ Para otros usos de este término, véanse Rotación de cultivos y Rotación estelar. Para el movimiento que hace la Tierra al girar, véase Rotación de la Tierra. Rotación de la Tierra. Rotación es el movimiento de cambio de orientación de un cuerpo o un sistema de referencia de forma que una línea (llamada eje de rotación) o un punto permanece fijo. La rotación de un cuerpo se representa mediante un operador que afecta a un conjunto de puntos o vectores. El movimiento rotatorio se representa mediante el vector velocidad angular \boldsymbol\omega, que es un vector de carácter deslizante y situado sobre el eje de rotación. Cuando el eje pasa por el centro de masa o de gravedad se dice que el cuerpo «gira sobre sí mismo». Pendulum 30deg.gif Pendulum 220deg.gif La rotación también puede ser oscilatoria, como en el péndulo (izquierda). Los giros son completos sólo cuando la energía es lo suficientemente alta (derecha). El gráfico superior muestra la trayectoria en el espacio fásico. En ingeniería mecánica, se llama revolución a una rotación completa de una pieza sobre su eje (como en la unidad de revoluciones por minuto), mientras que en astronomía se usa esta misma palabra para referirse al movimiento orbital de traslación de un cuerpo alrededor de otro (como los planetas alrededor del Sol). Índice [ocultar] 1 Rotación en física 1.1 Concepto de rotación y revolución 1.2 Movimiento rotatorio 1.2.1 Rotación infinitesimal 1.2.2 Velocidad angular 1.3 Dinámica de rotación 1.4 Eje de rotación 2 Rotación en matemáticas 2.1 Introducción matemática 2.2 Rotaciones en el plano 2.2.1 Expresión matricial 2.2.2 Expresión mediante números complejos 2.3 Teorema de rotación de Euler 2.4 Rotaciones en el espacio 2.4.1 Expresión vectorial 2.4.2 Expresiones matriciales 2.4.3 Expresiones vectoriales 2.4.4 Ángulos de Euler 2.4.5 Parámetros de Euler-Rodrigues y cuaterniones 2.5 Teoría de grupos 2.5.1 Rotaciones frente a traslaciones 2.5.2 Rotaciones frente a reflexiones e inversiones 3 Percepción de las rotaciones 4 Véase también 5 Referencias Rotación en física[editar] Concepto de rotación y revolución[editar] Animación de dos objetos orbitando alrededor de un centro de masas común, ejemplo de revolución. Ejemplo de rotación. Ejemplo de revolución. El movimiento de la estructura de una noría corresponde a un movimiento de rotación. Por el contrario, las barquillas de la noria realizan un movimiento de traslación o revolución con trayectoria circular. En astronomía es habitual distinguir entre el movimiento de rotación y el de revolución con los siguientes sentidos: La rotación de un cuerpo alrededor de un eje (exterior o interior al cuerpo) corresponde a un movimiento en el que los distintos puntos del cuerpo presentan velocidades que son proporcionales a su distancia al eje. Los puntos del cuerpo situados sobre el eje (en el caso de que éste sea interior al cuerpo) permanecen en reposo. La orientación del cuerpo en el espacio cambia continuamente durante la traslación. Un ejemplo de rotación es el de la Tierra alrededor de su propio eje de rotación, con un período de rotación de un día sidéreo. La revolución de una partícula o de un cuerpo extenso corresponde a un movimiento de traslación del cuerpo alrededor de otro. Un ejemplo de revolución es el de la Tierra alrededor del Sol, con un periodo de revolución de un año. La distinción entre rotación y revolución está asociada con la existente entre rotación y traslación de un cuerpo extenso. Si la velocidad de traslación es constante (v=cte), cada uno de los puntos del sólido recorrerá una trayectoria rectilínea con celeridad constante y todas esas trayectorias serán paralelas entre sí (movimiento de traslación uniforme). Pero, en general, la velocidad de traslación no tiene por que ser constante y la trayectoria puede ser curvilínea. Las trayectorias recorridas por los distintos puntos del cuerpo pueden ser circunferencias, todas ellas del mismo radio (congruentes) aunque de distinto centro. Esta situación se presenta en una noria de feria de eje horizontal, como se muestra en la figura: la armadura de la noria gira en torno al eje (rotación), pero las barquillas suspendidas de dicha armadura, prescindiendo de pequeñas oscilaciones pendulares, experimentan una traslación con trayectorias circulares. Movimiento rotatorio[editar] Rotación infinitesimal[editar] En una rotación en un ángulo infinitesimal δθ, se puede tomar cos δθ ≈ 1 y sen δθ ≈ δθ, de modo que la expresión de la rotación plana pasa a ser: \mathbf{r}'= \mathbf{r} + \delta\theta (\mathbf{u}\times\mathbf{r}) Si se componen dos rotaciones infinitesimales y, por ello, se descartan los términos de orden superior al primero, se comprueba que poseen la propiedad conmutativa, que no tienen las rotaciones tridimensionales finitas. Matemáticamente el conjunto de las rotaciones infinitesimales en el espacio euclideo forman el álgebra de Lie \mathfrak{so}(3), asociada al grupo de Lie SO(3) Velocidad angular[editar] Artículo principal: Cinemática del sólido rígido Dado un sólido rígido que rota alrededor de un eje, la velocidad lineal v de una partícula se puede expresar a partir de la velocidad angular ω: \mathbf{v} = \frac{d\mathbf{r}}{dt} = \boldsymbol\omega \times \mathbf{r} Mientras que la aceleración a es: \mathbf{a} = \frac{d\mathbf{v}}{dt} = \boldsymbol{\alpha} \times \mathbf{r} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r}) Si el sólido rígido además de rotar alrededor de un eje tiene un movimiento adicional de traslación con velocidad instantánea V entonces las fórmulas anteriores deben substituirse por: \mathbf{v} = \frac{d\mathbf{r}}{dt} = \boldsymbol\omega \times \mathbf{r} + \mathbf{V} \mathbf{a} = \frac{d\mathbf{v}}{dt} = \boldsymbol{\alpha} \times \mathbf{r} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r}) + 2\boldsymbol\omega \times \mathbf{V} + \frac{d\mathbf{V}}{dt} Dinámica de rotación[editar] La velocidad angular de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el sólido y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del sólido a alterar su movimiento de rotación. La energía cinética de rotación se escribe: E_c = \frac{1}{2} \boldsymbol\omega \cdot (\mathbf{I} \boldsymbol\omega) siendo \scriptstyle \mathbf{I} el tensor momento de inercia. La expresión del teorema del trabajo en movimientos de rotación se puede expresar así: \Delta E_c=\mathbf{M}\cdot\Delta\boldsymbol{\theta} de modo que, la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado (\Delta\theta). Eje de rotación[editar] Si bien se define la rotación como un movimiento de rotación alrededor de un eje, debe tenerse presente que dicho eje de rotación puede ir cambiando su inclinación a lo largo del tiempo. Así sucede con eje de rotación terrestre y en general el eje de rotación de cualquier sólido en rotación que no presente simetría esférica. Para un planeta, o en general cualquier sólido en rotación, sobre el que no actúa un par de fuerza el momento angular se mantiene constante, aunque eso no implica que su eje de rotación sea fijo. Para una peonza simétrica, es decir, un sólido tal que dos de sus momentos de inercia principales sean iguales y el tercero diferente, el eje de rotación gira alrededor de la dirección del momento angular. Los planetas con muy buena aproximación son esferoides achatados en los polos, lo cual los convierte en una peonza simétrica, por esa razón su eje de giro experimenta una rotación conocida como precesión. La velocidad angular de precesión viene dada por el cociente entre el momento angular de rotación y el menor de los momentos de inercia del planeta: \dot\phi_{prec} = \frac{L}{I_{\min}} El el caso de existencia de asimetría axial el planeta es una peonza asimétrica y además el eje de giro puede realizar un movimiento de nutación. Rotación en matemáticas[editar] Introducción matemática[editar] El tratamiento detallado de las rotaciones ha sido objeto de numerosos trabajos matemáticos, que abordan el problema desde diversos puntos de vista y grados de sofisticación: cuaterniones, matrices, operadores vectoriales, teoría de grupos... Todos estos enfoques son matemáticamente equivalentes y se pueden derivar unos de otros, salvo en algunos aspectos concretos y posibles resultados redundantes, y la elección de uno u otro depende del problema concreto. Con la llegada de la robótica y los gráficos informáticos, la matemática de las rotaciones ha cobrado un nuevo impulso y ha pasado a ser una materia de estudio muy activo, con particular énfasis en el enfoque basado en cuaterniones. En matemáticas las rotaciones son transformaciones lineales que conservan las normas (es decir, son isométricas) en espacios vectoriales en los que se ha definido una operación de producto interior y cuya matriz tiene la propiedad de ser ortogonal y de determinante igual a ±1. Si el determinante es +1 se llama rotación propia y si es −1, además de una rotación propia hay una inversión o reflexión y se habla de rotación impropia.1 La conservación de la norma es equivalente a la conservación del producto interior, que se puede expresar como: \mathcal{R}\mathbf{a}\cdot\mathcal{R}\mathbf{b} =\mathbf{a}\cdot\mathbf{b} Consecuencia de ella es que las distancias y las formas también se conservan. Como parámetro que determina la rotación se puede usar un vector (que tiene carácter deslizante) del eje de rotación y de longitud proporcional al ángulo de rotación. Sin embargo, lo normal es separar este vector en el ángulo y un vector unitario, lo que en el espacio da cuatro parámetros.2 Como consecuencia hay dos formas de representar una única rotación, pues \mathcal{R}(\theta,\mathbf{a}) = \mathcal{R}(-\theta,-\mathbf{a}) Rotaciones en el plano[editar] Cambio de base o rotación de un vector. Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes: \mathbf A=\begin{bmatrix} A_x \\ A_y \end{bmatrix} La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector: \mathcal{R} \mathbf{A} = \mathbf{A}' Expresión matricial[editar] En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente: \mathcal{R} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{bmatrix} Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo \theta en sentido antihorario: \begin{bmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{bmatrix} \begin{bmatrix} A_x \\ A_y \end{bmatrix} = \begin{bmatrix} A'_x \\ A'_y \end{bmatrix} siendo A'_x = A_x \cos\theta - A_y\sin\theta\, A'_y = A_x \sin\theta + A_y\cos\theta\, las componentes del nuevo vector después de la rotación. Expresión mediante números complejos[editar] Las rotaciones en el plano pueden tratarse igualmente mediante números complejos, ya que eiα es una rotación de ángulo a: (x,y)\in \R^2 \rightarrow x+iy = \rho e^{i\phi}\in \mathbb{C} \xrightarrow{\mathrm{rot}} z = e^{i\alpha}(\rho e^{i\phi})\rightarrow (\mathrm{Re}(z),\mathrm{Im}(z)) = (\rho\cos(\phi+\alpha),\rho\sin(\phi+\alpha))\in \R^2 (\rho\cos(\phi+\alpha),\rho\sin(\phi+\alpha))= (x\cos(\alpha)-y\sin(\alpha),x\sin(\alpha)+y\cos(\alpha)) El grupo de rotaciones en dos dimensiones es isomorfo al grupo de Lie, ortogonal especial SO(2) que a su vez es isomorfo al grupo unitario U(1). Teorema de rotación de Euler[editar] En matemáticas, el teorema de rotación de Euler dice que cualquier rotación o conjunto de rotaciones sucesivas puede expresarse siempre como una rotación alrededor de una única dirección o eje de rotación principal. De este modo, toda rotación (o conjunto de rotaciones sucesivas) en el espacio tridimensional puede ser especificada a través del eje de rotación equivalente definido vectorialmente por tres parámetros y un cuarto parámetro representativo del ángulo rotado. Generalmente se denominan a estos cuatro parámetros grados de libertad de rotación. Rotaciones en el espacio[editar] Las tres rotaciones planas de los ángulos de Euler. En la primera el eje es z, que apunta hacia arriba y gira los ejes x e y; en la segunda el eje es x, que apunta hacia el frente y que inclina el eje z, y en la última de nuevo el eje es z. Las rotaciones tridimensionales revisten especial interés práctico por corresponderse con la geometría del espacio físico en que vivimos (naturalmente siempre que se consideren regiones de escala mediana, ya que para distancias grandes la geometría no es estrictamente euclídea). En tres dimensiones conviene distinguir entre las rotaciones planas o rectangulares, que son aquellas en las que el vector rotado y el que determina el eje de giro forman un ángulo recto, y las cónicas, en las que el ángulo entre estos vectores no es recto. Las rotaciones planas son de tratamiento matemático más simple, pues se pueden reducir al caso bidimensional descrito más arriba, mientras que las cónicas son mucho más complejas y por lo general se tratan como una combinación de rotaciones planas (especialmente los ángulos de Euler y los parámetros de Euler-Rodrigues). Expresión vectorial[editar] La expresión vectorial de las rotaciones cónicas es: \mathbf{r}' = \mathbf{r} \cos\theta + (\mathbf{u} \times \mathbf{r})\sin\theta + \mathbf{u} (\mathbf{u} \cdot \mathbf{r}) (1 - \cos\theta) donde: \mathbf{r}, \mathbf{r}' representan los vectores posición de un punto antes y después de la operación de rotación. \mathbf{u} es un vector unitario que coincide con la dirección de eje de giro. \theta\in[0,2\pi) es el valor del ángulo girado. \cdot, \times, denotan respectivamente el producto escalar y el producto vectorial. Expresiones matriciales[editar] Matricialmente este producto se puede escribir de varias maneras, bien como matriz ortogonal: \mathbf{r}'=\mathcal{R}_{\theta,\mathbf{u}} (\mathbf{r})\quad \Leftrightarrow \quad \begin{bmatrix} x'\\ y'\\ z' \end{bmatrix} = \begin{bmatrix}C^2+S^2(u_x^2- u_y^2- u_z^2) & 2S( Su_x u_y-C u_z) & 2S(S u_x u_z + C u_y) \\ 2S(S u_x u_y+C u_z) & C^2+S^2( u_y^2- u_x^2- u_z^2) & 2S(S u_y u_z - C u_x) \\ 2S(S u_x u_z-C u_y) & 2S(S u_y u_z+C u_x) & C^2+S^2( u_z^2- u_x^2- u_y^2) \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} Donde: \mathbf{r} = (x,y,z), \mathbf{r}' = (x',y',z') \mathbf{u} = (u_x,u_y,u_z) C=\cos(\theta/2), S=\sin(\theta/2) Puede comprobarse con un poco de álgebra rutinaria que la matriz anterior tiene como autovalores: \{1, C+iS, C-iS\}= \{1, e^{i\theta}, e^{-i\theta}\} La dirección principal (recta generada por un vector propio) asociaciada al autovalor 1 es precisamente el vector \scriptstyle \mathbf{u} que da la dirección de eje de giro. Expresiones vectoriales[editar] Se puede describir el movimiento de rotación cónica con operadores vectoriales que, al contrario que las expresiones matriciales, son independientes de las coordenadas. Así,3 \mathbf{r}' = ((1 -\cos \theta)\mathbf{uu}+ \cos \theta + \mathop{\mathrm{sen}} \theta \tilde{\mathbf{u}}) \cdot \mathbf{r} donde la expresión entre paréntesis funciona como operador y \tilde{\mathbf{u}}= \mathbf{I}\times \mathbf{u}, de modo que \tilde{\mathbf{u}}\cdot \mathbf{r}=\mathbf{u}\times\mathbf{r}.4 Hay ciertos casos especiales de este operador: \tilde{\mathbf{u}} es una rotación plana de (1/2)π rad. La aplicación sucesiva de este operador da \tilde{\mathbf{u}}^2=-1, \tilde{\mathbf{u}}^3=-\tilde{\mathbf{u}}, \tilde{\mathbf{u}}^4=1, \tilde{\mathbf{u}}^5=\tilde{\mathbf{u}}, etc., con un comportamiento parecido a la unidad imaginaria (i).5 Es un operador hemisimétrico y en coordenadas castesianas su matriz es: \begin{pmatrix} {0} & -u_z & u_y\\ u_z & {0} & -u_x\\ -u_y & u_x &{0}\\ \end{pmatrix} \cos \theta + \sin \theta \tilde{\mathbf{u}} es una rotación plana de ángulo θ. Una notación alternativa es \mathrm{e}^{\tilde{\mathbf{u}}\theta} (por similitud con los números complejos). La forma matricial de este operador en los ejes cartesianos principales es particularmente sencilla; por ejemplo, para i es: \mathcal{R} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin\theta & \cos \theta\end{bmatrix} 2\mathbf{uu}-1 es una rotación cónica binaria (de π rad). Una rotación cónica arbitraria de ángulo θ se puede representar con dos rotaciones binarias, perpendiculares a \mathbf{u} y que forman un ángulo (1/2)θ;6 la manipulación de este par de rotaciones binarias (o, de modo equivalente, de dos reflexiones) se puede tomar como la base para la descripción mediante los parámetros de Euler-Rodrigues. Así, el segundo de estos ejes se obtiene mediante una rotación plana del primero con \cos \frac{1}{2}\theta + \mathop{\mathrm{sen}} \frac{1}{2}\theta \tilde{\mathbf{u}}, que da los cuatro parámetros: \lambda =u_x \mathop{\mathrm{sen}} \theta/2\qquad \mu =u_y \sin \theta/2\qquad \nu=u_z \sin \theta/2\qquad \rho = \cos\theta/2 Ángulos de Euler[editar] Artículo principal: Ángulos de Euler Mediante los ángulos de Euler se puede representar una rotación cualquiera con una sucesión de tres rotaciones planas alrededor de tres ejes ortogonales. No hay acuerdo sobre los tres ejes concretos y en la literatura científica aparecen diversos convenios; hay, en concreto, 12 posibilidades, pero lo más habitual es que se tomen zyz y zxz. A estos 12 convenios hay que añadir posibles variaciones en el signo, orientación relativa de ejes (horario o antihorario) y punto de vista (operación en vectores o transformación de coordenadas).7 Los ángulos de Euler fueron el sistema más popular en los siglos XIX y XX para representar las rotaciones, pues permiten modelizar fácilmente varios sistemas mecánicos, como los trompos, los giroscopios, los barcos y los aviones. En el caso del trompo, los ejes se corresponden con la precesión, la nutación y la rotación. En los aviones se toman como ejes xyz, de modo que se correspondan con el alabeo (o balanceo en barcos), el cabeceo y la guiñada; este convenio específico de ejes se llama también ángulos de navegación o de Tait-Bryan. Los ángulos de Euler presentan una singularidad cuando el ángulo del segundo giro es 0 o π, pues en tal caso el primer ángulo y el segundo pasan a quedar indefinidos, y solo está definida su suma, si el ángulo es 0. Con ello se pierde un grado de libertad, lo que en los dispositivos mecánicos que combinan varios ejes, como los giroscopios, puede conducir a un bloqueo del sistema, conocido como bloqueo de cardán (en inglés, gimbal lock). Matemáticamente, es posible evitar estas singularidades con sistemas de cuatro parámetros, como los parámetros de Euler-Rodrigues (o cuaterniones). Parámetros de Euler-Rodrigues y cuaterniones[editar] Los cuaterniones proporcionan un método para representar rotaciones que no presentan singularidades a costa de ser redundantes. Pueden introducirse axiomáticamente o derivarse a partir de rotaciones vectoriales, en especial mediante la construcción de Euler-Rodrigues.8 Históricamente, los cuatro parámetros que forman los cuaterniones fueron introducidos de modo independiente y con diferentes tratamientos matemáticos y geométricos por Gauss, Rodrigues y Hamilton, entre otros, aunque aparentemente Euler, a pesar del nombre, los desconocía. Rodrigues llegó a ellos mediante trigonometría esférica como una combinación de reflexiones; Hamilton, poco después, lo formuló de modo axiomático como una extensión de los números complejos. En mecánica cuántica también se llegó a ellos con las matrices de Pauli. En tres dimensiones existe una construcción similar a la de los números complejos de módulo unidad para representar las rotaciones en el plano. La construcción clave reside en identificar los vectores tridimensionales con números cuaterniónicos con parte real nula, y usar las tres componentes como coeficientes de la parte no real. La rotación se puede representar como un producto conjugado por un cuaternión unitario obtenido por exponenciación de un cuaternión igual al producto del ángulo girado por el cuaternión que representa al eje de giro. Dado un vector tridimensional \scriptstyle \mathbf{v} rerepsentable como un número cuaterniónico con parte real nula, y una rotación tridimensional dada por un giro \scriptstyle \alpha en torno al eje \scriptstyle \mathbf{n} se puede representar el vector girado resultante como: \begin{cases} \mathbf{v}\in \R^3 \mapsto v=0+v_x\mathbf{i}+v_y\mathbf{j}+v_z\mathbf{k} \in\mathbb{H}\\ \mathbf{v}' = R_{\mathbf{n},\alpha}(\mathbf{v}) \mapsto e^{\alpha(n_x\mathbf{i}+n_y\mathbf{j}+n_z\mathbf{k})/2} \cdot v \cdot e^{-\alpha(n_x\mathbf{i}+n_y\mathbf{j}+n_z\mathbf{k})/2} \end{cases} Este enfoque está relacionado con el álgebra geométrica y los vectores i, j y k siguen las reglas algebraicas de los cuaterniones (i2 = −1, etc.). El producto de dos rotaciones viene dado, en términos de vectores ordinarios, por:9 [0, \mathbf{A}][0, \mathbf{B}] = [-\mathbf{A}\cdot\mathbf{B}, \mathbf{A}\times\mathbf{B}] donde [a, b] representa un cuaternión con parte real a y parte no real b. Teoría de grupos[editar] Una rotación de un sexto de vuelta completa (2π/6) alrededor de un eje que atraviesa la pantalla deja igual la molécula de benceno, por lo que hay una simetría rotacional (entre otras). En teoría de grupos, la rotación es una de las posibles transformaciones que se pueden aplicar a un sistema o una figura geométrica, que permiten determinar la simetría de redes cristalográficas, orbitales atómicos y moléculas, y por tanto parte de sus propiedades físico-químicas. Otras tranformaciones son la traslación, la reflexión y la inversión. Rotaciones frente a traslaciones[editar] En mecánica se demuestra que el movimiento del sólido rígido se puede descomponer en una rotación y una traslación. Ambas trasformaciones son isométricas, como corresponde al hecho de que el sólido es rígido, pero en la rotación, al contrario que en la traslación, hay al menos un punto fijo. El conjunto de estas transformaciones forma un grupo llamado grupo euclidiano que es el grupo de isometría del espacio euclidiano tridimensional. Cada elemento g de este grupo euclidiano se puede representar de manera única como:10 g \to \begin{pmatrix} R & \mathbf{d}\\ \mathbf{0} & 1 \end{pmatrix} \in \mathrm{GL}(4,\R) donde R es una matriz de 3x3 que representa una rotación y d las componentes del vector de tres componentes que representa el desplazamiento. Por tanto esta manera de representar el grupo es una representación lineal sobre un espacio vectorial de dimensión cuatro. Rotaciones frente a reflexiones e inversiones[editar] Estas tres transformaciones se llaman tranformaciones puntales pues dejan un punto fijo, y están estrechamente relacionadas. Así, dos reflexiones según dos planos equivalen a una rotación. La composición de dos rotaciones tridimensionales es otra rotación, por lo que estas forman un grupo, llamado O(3) y que incluye las reflexiones. Las rotaciones propias son un subgrupo, llamado SO(3), pero no las rotaciones impropias, pues dos de ellas equivalen a una rotación propia. Percepción de las rotaciones[editar] Resultado. Imagen original de la composición. La imagen muestra un artificio para crear la ilusión de una rotación en 3D a partir de una imagen en 2D. Está formada por partes restringidas una detrás de otra, de modo que nuestro cerebro interpreta como una rotación de acuerdo a los datos que sobre el objeto (la cabeza) retiene nuestra memoria. Véase también[editar]

simetría central

Simetría central Spanish Language Wiki.svg Este artículo o sección sobre matemáticas necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 26 de junio de 2012. También puedes ayudar wikificando otros artículos. La simetría respecto de un punto se llama simetría central y los puntos correspondientes, homólogos. En una simetría central, los segmentos homólogos son iguales y la medida de los ángulos correspondientes también son iguales. Dos puntos P y P’ son simétricos respecto del centro de simetría O cuando OP = OP', esto es P y P' equidistan del centro de simetría.1 Ejemplo 1: Dibuja el triángulo simétrico respecto del centro O del triángulo dado ABC. Ejemplo1.JPG Índice [ocultar] 1 Propiedades 2 Simetría central y coordenadas 2.1 En el espacio tridimensional 3 Composición de simetrías 3.1 Con el mismo centro 3.2 Con distinto centro 4 Referencias y fundamentos Propiedades[editar] La imagen simétrica central de un segmento es otro segmento de igual longitud; si en el centro de simetría está en un segmento simetrizable, es simétrico de sí mismo, llamado punto doble La imagen de un triángulo, mediante simetría central, es otro triángulo congruente con el primero. La imagen de un polígono, mediante simetría central, es otro polígono congruente con el primero. Los polígonos regulares con un número par de lados tienen como centro de simetría su centro geométrico (baricentro); de modo que a cualquier punto de este polígono, le corresponde un homólogo que está en el mismo polígono.2 El centro de un triángulo equilátero no es centro de simetría, en el sentido de que reproduzca la misma figura; por decir el homólogo de un vértice sale del lado opuesto. La misma situación en el caso de un tetraedro regular, su centro geométrico no es centro de simetría.3 El centro de un cuadrado es centro de simetría de la figura; de igual manera, el centro de un cubo es centro de simetría del sólido. El centro de la esfera lo es también centro de simetría. Cualquier punto cumple las dos siguientes condiciones: A y A’ están alineados: la recta que los une pasa por O. La distancia de O al punto A es igual que la de O al transformado A’ Simetría central y coordenadas[editar] Estos triángulos son simétricos respecto del centro O. Para pasar de un punto a su simétrico se cambia el signo de las coordenadas: Si P =(x,y) entonces P’=(-x,-y). Coordenadas de los puntos Coordenadas de sus simétricos A=(3, 1) A=(-3, -1) B=(1, 2) B=(-1, -2) C=(2, -1) C=(-2, 1) Dos puntos P=(x,y) y P’=(x’,y’) simétricos respecto de origen de coordenadas tienen sus abscisas y ordenadas opuestas. Las ecuaciones de la simetría central son: x’ = -x, y’ = -y En el espacio tridimensional[editar] Dado un punto P(x, y, z) y centro de simetría el origen de coordenadas el simétrico de P es el punto P' (-x, -y, -z) Dado un punto P ( en el plano o en el espacio ℝ3 ) y el centro de simetría Q, se hallan las coordenadas del simétrico P', mediante la ecuación de vectores 2Q = P + P', o bien: P' = 2Q - P, igualando las coordenadas hómólogas, generizable a cualquier espacio euclídeo.4 Composición de simetrías[editar]

simetria axial

Simetría axial

(Redirigido desde «Simetria axial»)

Para los seres vivos, véase Simetría radial (biología).

Problema axisimétrico respecto a un eje, la situación en todos los semiplanos Π, como el de la figura es idéntica.

La simetría axial (también llamada rotacional o radial o cilíndrica) es la simetría alrededor de un eje, de modo que un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierta mediatriz y conteniéndolo presentan idénticas características.También puede decirse que es una isometría indirecta e involutiva.

Dada una recta se llama simetría axial de eje al movimiento que transforma a un punto P en otro punto P' verificando que:

El segmento PP' es perpendicular a $\scriptstyle e$ .
Los puntos P y P' equidistan del eje $\scriptstyle e$ .

Dicho de otra forma el eje

\scriptstyle e

es la mediatriz del segmento PP'

La simetría axial no solo se presenta entre un objeto y su reflexión, pues muchas figuras que mediante una línea pueden partirse en dos secciones que son simétricas con respecto a la línea. Estos objetos tienen uno (o más) ejes de simetría.

La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.

A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica. En este caso: La simetría axial se puede dar también en un objeto con respecto de uno o más ejes de simetría.

Si se doblara la figura sobre el eje de simetría trazado, se podría observar con toda claridad que los puntos de las partes opuestas coinciden, es decir, ambas partes son congruentes.

Definición de movimiento plano

De entre los posibles movimientos de un sólido rígido, se dice que un sólido “2” realiza un movimiento plano respecto a un sólido “1” si los desplazamientos de todos sus puntos son permanentemente paralelos a un plano fijo en el sistema de referencia ligado al sólido 1. Este plano se denomina plano director,

Π D

del movimiento plano.

Así, por ejemplo, el movimiento que realiza el chasis de un coche, respecto a la calzada por la que éste circula, es un movimiento plano.

También lo es el movimiento de una de sus ruedas cuando el coche avanza en línea recta. Sin embargo, en ese caso, el plano director no es el plano de la calzada, sino uno perpendicular a ella.

Cualquier plano paralelo a un plano director del movimiento {21} funciona también como plano director de dicho movimiento, por lo que ese término designa realmente a toda la familia de planos paralelos, caracterizados por una perpendicular común. Esta dirección normal a la familia de planos directores puede tomarse siempre como eje OZ (o cualquier otra dirección fija que nos convenga) y el vector unitario normal a los planos directores puede ser denotado como $\vec{k}$

Matemáticamente tenemos que, para todo punto del sólido debe cumplirse en todo instante que

$\vec{v}^P_{21}\cdot\vec{k}=0\qquad\forall t,\ \forall P$

2 Propiedades del movimiento plano

Un movimiento plano de un sólido satisface, entre otras, las siguientes propiedades:

1) Las velocidades de todos los puntos del sólidos se encuentran contenidas en planos paralelos: Es la condición definitoria del movimiento plano.
2) Las aceleraciones de todos los puntos son siempre paralelas al plano director: Puesto que la identidad anterior se cumple en cada instante, podemos derivar en ella respecto al tiempo

$0 = \left.\frac{\mathrm{d} }{\mathrm{d}t}(\vec{v}^P_{21}\cdot\vec{k})\right|_1=\left.\frac{\mathrm{d} }{\mathrm{d}t}(\vec{v}^P_{21})\right|_1\cdot\vec{k} = \vec{a}^P_{21}\cdot\vec{k}$

3) La trayectoria de cada uno de los puntos es plana: Puesto que la velocidad y la aceleración de cada punto son tangentes al plano director, el vector binormal de cada trayectoria es siempre perpendicular al plano y por tanto constante.

4) La velocidad angular del movimiento {21} es perpendicular al plano director (o nula): Por tratarse de un movimiento rígido, para cualesquiera dos puntos del sólido 2 se cumple

$\vec{v}^Q_{21}=\vec{v}^P_{21}+\vec{\omega}_{21}\times\overrightarrow{PQ}$

Multiplicando aquí escalarmente por el vector normal al plano director

$\vec{k}\cdot\vec{v}^Q_{21}=\vec{k}\cdot\vec{v}^P_{21}+\vec{k}\cdot(\vec{\omega}_{21}\times\overrightarrow{PQ})$ $\Rightarrow$ $0 = 0 + (\vec{k}\times\vec{\omega}_{21})\cdot\overrightarrow{PQ}$

Puesto que esta identidad debe cumplirse para cualquier par de puntos, la única posibilidad es que

$\vec{k}\times\vec{\omega}_{21}=\vec{0}\qquad\Rightarrow\qquad\begin{cases} \vec{\omega}_{21}=\vec{0} & \\ \mbox{ o } & \\ \vec{\omega}_{21}\parallel\vec{k} &\end{cases}\qquad\Rightarrow\qquad\vec{\omega}_{21}=\omega_{21}\vec{k}$

Esto permite tratar a la velocidad angular como una cantidad escalar, puesto que su dirección es conocida. El sentido de la velocidad angular lo da el signo de la cantidad escalar

ω 21

5) La aceleración angular del movimiento {21} es perpendicular al plano director: Es consecuencia inmediata de que la velocidad angular posea dirección constante

$\vec{\alpha}_{21}=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1=\frac{\mathrm{d}\omega_{21}}{\mathrm{d}t}\vec{k}=\alpha_{21}\vec{k}$

6) Son compatibles con un movimiento plano los movimientos instantáneos {21} de reposo, traslación o rotación, pero no el helicoidal: Si $\vec{\omega}_{21}=\vec{0}$ entonces el movimiento {21} es un estado de reposo o es una traslación.; Si la velocidad angular no es nula, la velocidad de deslizamiento vale 0

$v_d = \frac{\vec{v}^P_{21}\cdot\vec{\omega}_{21}}{|\vec{\omega}_{21}|}=\vec{v}^P_{21}\cdot\vec{k}=0$

y por tanto en ese caso el movimiento es una rotación.

Cabe señalar que el movimiento plano más frecuente es una sucesión de rotaciones instantáneas, a veces con algún instante aislado de traslación o reposo. No obstante, son también destacables por su importancia los siguientes dos casos particulares de movimiento plano: la traslación permanente paralela a un plano fijo, y la rotación alrededor de un eje fijo.

7) Las distribuciones de velocidades en planos paralelos al plano director son idénticas entre sí: Si el movimiento es una traslación, evidentemente las distribuciones son idénticas, ya que todos los puntos tienen la misma velocidad.; Si se trata de una rotación, el eje instantáneo de rotación es perpendicular al plano director, y por tanto, las distribuciones de las velocidades en planos perpendiculares a este eje (y paralelos al plano director) son idénticas.; Esto quiere decir que para estudiar el movimiento plano basta con considerar lo que ocurre en uno de sus planos paralelos al plano director. Esto no implica que el sólido sea cilíndrico (esto es, que el sólido real no tiene por qué tener la misma forma en todos los planos paralelos al director).; El campo de velocidades se puede expresar en la forma

$\vec{v}^P_{21}=\vec{v}^O_{21}+\omega_{21}\vec{k}\times\overrightarrow{OP}$

donde O y P son los dos puntos del mismo plano director. Gráficamente, el vector $\vec{k}\times\overrightarrow{OP}$ representa un giro del vector $\overrightarrow{OP}$ un ángulo de

π / 2

en sentido antihorario dentro del plano director.

8) Las distribuciones de aceleraciones en planos paralelos al plano director son idénticas entre sí: Si tenemos puntos P y Q situados sobre la misma recta normal al plano director,

$\overrightarrow{PQ}=b\vec{k}\qquad\vec{a}^Q_{21}=\vec{a}^P_{21}+\overbrace{\vec{\alpha}_{21}\times\overrightarrow{PQ}}^{=\vec{0}}+\vec{\omega}_{21}\times(\overbrace{\vec{\omega}_{21}\times\overrightarrow{PQ}}^{=\vec{0}})=\vec{a}^P_{21}$

El campo de aceleraciones puede simplificarse en el caso del movimiento plano a la expresión

$\vec{a}^P_{21}=\vec{a}^O_{21}+\alpha_{21}\vec{k}\times\overrightarrow{OP}+\omega_{21}^2\vec{k}\times(\vec{k}\times\overrightarrow{OP})$

siendo O y P dos puntos del mismo plano. El doble producto vectorial del segundo miembro corresponde, gráficamente, a una doble rotación de

π / 2

, esto es

$\vec{k}\times(\vec{k}\times\overrightarrow{OP})=-\overrightarrow{OP}$

lo que reduce la expresión del campo de aceleraciones a

$\vec{a}^P_{21}=\vec{a}^O_{21}+\alpha_{21}\vec{k}\times\overrightarrow{OP}-\omega_{21}^2\overrightarrow{OP}$

9) Un movimiento plano tiene tres grados de libertad: Un movimiento rígido general tiene 6 grados de libertad, especificados por las tres componentes de la velocidad angular y las tres componentes de la velocidad de un punto. En un movimiento plano, la velocidad angular tiene una sola componente que puede variar, la normal al plano, y la velocidad de un punto tiene dos, tangentes al mismo plano

$\vec{\omega}_{21}=\omega_{21}\vec{k}$ $\vec{v}^O_{21}=v^O_x\vec{\imath}+v^O_y\vec{\jmath}$

Las especificación de esos 3 valores determina completamente el movimiento del sólido, que por tanto tiene 3 grados de libertad. En términos de variables, un movimiento plano queda descrito por la evolución temporal de dos coordenadas de un punto y del ángulo que forman los ejes de los triedros “2” y “1”.

θ

es el ángulo que forma en cada instante el eje

O X 2

con el

O X 1

(medido desde el

O X 1

O X 2

en sentido antihorario), la velocidad angular y la aceleración angular instantáneas vienen dadas por

$\vec{\omega}_{21}=\dot{\theta}\vec{k}$ $\vec{\alpha}_{21}=\ddot{\theta}\vec{k}$

3 Centro instantáneo de rotación (C.I.R.)

3.1 Definición

En el caso de que el movimiento {21} consista en una rotación, se define el centro instantáneo de rotación (CIR) del movimiento plano {21},

I 21

, como el punto de intersección del eje instantáneo de rotación con el plano director de dicho movimiento.

Hay que destacar que, en general, el CIR representa un punto material del sólido “2” diferente en cada instante. Lo mismo ocurre con el sólido “1”: el CIR

I 21

coincide con un punto material diferente en cada instante.

Consideremos, por ejemplo, el caso de un disco “2” que rueda sin deslizar sobre una superficie horizontal “1”. Es éste un movimiento plano, siendo el plano director uno normal a la superficie horizontal y paralelo a la superficie del disco. El EIR del movimiento {21} es una recta tangente al plano horizontal y que pasa por el punto de contacto del disco con el suelo. El CIR

I 21

en cada instante será el punto de contacto del disco con el suelo. Sin embargo, no hay ningún átomo del disco ni del suelo que coincida en todo momento con el CIR, sino que es uno diferente en cada instante.

En el caso de un movimiento de traslación, el centro instantáneo de rotación no corresponde a ningún punto del espacio, ya que no hay eje instantáneo de rotación. No obstante, puede considerarse un movimiento de traslación como un límite de movimientos de rotación con radios cada vez más grandes. Definiendo el CIR para un movimiento de traslación según este criterio, se encontraría en un punto del infinito, en la dirección dada por la perpendicular a la velocidad instantánea de traslación.

3.2 Propiedades

La velocidad del CIR es nula: Es consecuencia de que el CIR pertenezca al eje instantáneo de rotación.

$\vec{v}^{I_{21}}_{21}=\vec{0}$

Esto no implica que la aceleración del CIR sea nula. Puesto que

I 21

corresponde a un punto material distinto en cada instante, el valor de su velocidad no puede derivarse para obtener la aceleración. Podremos obtener, eso sí, la aceleración del punto material correspondiente empleando la expresión general del campo de aceleraciones. Así, para el caso de una rueda, la aceleración del punto de contacto con el suelo es radial y dirigida hacia el centro del disco.

La posición del CIR del movimiento {12} coincide con la del {21}: Por la fórmula de composición de velocidades

$\vec{v}^{I_{21}}_{12}=-\vec{v}^{I_{21}}_{21}=\vec{0}$ $\Rightarrow$ $I_{21}=I_{12}\,$

Por ello, se puede hablar indistintamente del CIR del movimiento {21} o del {12} sin importar el orden en que se enumeran los dos sólidos.

La distribución de velocidades posee simetría rotacional alrededor del CIR: De nuevo, es consecuencia de que se encuentre en el EIR:

3.3 Determinación del CIR

3.3.1 Procedimiento analítico

En el caso de una rotación, la posición del CIR de un movimiento puede hallarse analíticamente particularizando la fórmula de cálculo del EIRMD. Si A es un punto del plano director, con velocidad $\vec{v}^A_{21}$ , y $\vec{\omega}_{21}$ es la velocidad angular del movimiento, la posición relativa del CIR es

$\overrightarrow{AI}_{21}=\frac{\vec{\omega}_{21}\times\vec{v}^A_{21}}{\omega_{21}^2}=\frac{\vec{k}\times\vec{v}^A_{21}}{\omega_{21}}$

Vemos que efectivamente, cuando $\omega_{21}\to 0$ y el movimiento se reduce a una traslación, la posición del CIR se va al infinito según una dirección perpendicular a la velocidad de traslación.

Si no se conoce la velocidad angular, sino la velocidad de dos puntos A y B del mismo plano director, puede hallarse la velocidad angular a partir de la relación general

$\vec{v}^B_{21}-\vec{v}^A_{21}=\vec{\omega}_{21}\times\overrightarrow{AB}=\omega_{21}(\vec{k}\times\overrightarrow{AB})$

y de aquí resulta, proyectando y despejando

$\omega_{21}=\frac{\left(\overrightarrow{AB}\times(\vec{v}^B_{21}-\vec{v}^A_{21})\right)\cdot\vec{k}}{|\overrightarrow{AB}|^2}$

Sustituyendo en la expresión de arriba obtenemos la posición relativa del CIR respecto al punto A.

3.3.2 Procedimiento geométrico o gráfico

La posición del CIR también puede hallarse de forma sencilla geométricamente (teniendo el procedimiento geométrico su correspondiente versión analítica).

Suponemos que conocemos las velocidades de dos puntos del plano director, A y B. Clasificamos entonces el movimiento. Será una traslación si ambas velocidades son iguales y una rotación si son diferentes.

Caso de una traslación: Tomamos un punto cualquiera A, y trazamos la recta que pasa por A y es perpendicular a la velocidad $\vec{v}^A_{21}$ . El CIR $I 21$ se encontrará en el infinito según la dirección de esta recta (equivalentemente en cualquiera de sus dos “extremos”).

Caso de una rotación con $\vec{v}^A_{21}$ y $\vec{v}^B_{21}$ no paralelas: El CIR $I 21$ se encuentra en la intersección de la recta que pasa por A y es perpendicular a $\vec{v}^A_{21}$ con la recta que pasa por B y es perpendicular a $\vec{v}^B_{21}$ .

Caso de una rotación con $\vec{v}^A_{21}$ y $\vec{v}^B_{21}$ paralelas: En ese caso el CIR se encuentra en la recta que une los puntos A y B. Para hallar la posición sobre esta recta, observamos que la velocidad de diferentes puntos en una rotación es proporcional a la distancia al eje. Por tanto si sobre la gráfica trazamos con la misma escala la velocidad $\vec{v}^A_{21}$ con origen en A, y la velocidad $\vec{v}^B_{21}$ con origen en B, y trazamos la recta que pasa por los extremos de estos dos vectores, el punto donde corta a la recta AB es el CIR $I 21$ .

4 Composición de movimientos planos

Supongamos que tenemos tres sólidos “1”, “2” y “0” tales que los movimientos {20} y {01} son movimientos planos sobre el mismo plano director (o planos paralelos). En ese caso: La composición de dos movimientos planos paralelos entre sí es otro movimiento plano. Para todo punto P se verifica

$\vec{v}^P_{21}\cdot\vec{B}=\vec{v}^P_{20}\cdot\vec{B}+\vec{v}^P_{01}\cdot\vec{B}=0+0 = 0$

En este caso, la fórmula de composición de velocidades angulares se reduce a una suma de cantidades escalares

$\vec{\omega}_{ij}=\omega_{ij}\vec{k}\qquad\Rightarrow\qquad\omega_{21}=\omega_{20}+\omega_{01}$

y lo mismo ocurre para la composición de aceleraciones angulares

$\vec{\alpha}_{ij}=\alpha_{ij}\vec{k}\qquad\qquad\vec{\alpha}_{21}=\vec{\alpha}_{20}+\vec{\alpha}_{01}+\overbrace{\vec{\omega}_{01}\times\vec{\omega}_{20}}^{=\vec{0}}\qquad\Rightarrow\qquad\alpha_{21}=\alpha_{20}+\alpha_{01}$

Por su parte, la composición de velocidades y aceleraciones se convierte en suma de vectores en el plano, que en muchas ocasiones puede realizarse gráficamente. Así, para la composición de aceleraciones tenemos

$\vec{a}^P_{21}=\vec{a}^P_{20}+\vec{a}^P_{01}+2\omega_{01}\vec{k}\times\vec{v}^P_{20}$

Gráficamente, el resultado del producto vectorial $\vec{k}\times\vec{v}^P_{20}$ corresponde a girar el vector $\vec{v}^P_{20}$ un ángulo de

π / 2

en sentido antihorario.

4.1 Teorema de los tres centros

En un movimiento plano de tres sólidos en el que los tres movimientos relativos son rotaciones existen tres centros instantáneos de rotación,

I 21

I 20

I 01

. En general se verifica:

Teorema de los tres centros o de Aronhold-Kennedy: Los tres centros instantáneos de rotación $I 21$ , $I 20$ e $I 01$ están alineados.

Para demostrar el teorema aplicamos la fórmula de composición de velocidades al CIR

I 21

. Tenemos que

$\vec{0}=\vec{v}^{I_{21}}_{21}=\vec{v}^{I_{21}}_{20}+\vec{v}^{I_{21}}_{01}$

Las velocidades relativa y de arrastre de este punto valen

$\vec{v}^{I_{21}}_{20}=\vec{\omega}_{20}\times\overrightarrow{I_{20}I_{21}}=\omega_{20}\vec{k}\times\overrightarrow{I_{20}I_{21}}$ $\vec{v}^{I_{21}}_{01}=\vec{\omega}_{01}\times\overrightarrow{I_{01}I_{21}}=\omega_{01}\vec{k}\times\overrightarrow{I_{01}I_{21}}$

Sustituyendo en la velocidad absoluta queda

$\vec{0}=\vec{k}\times(\omega_{20}\overrightarrow{I_{20}I_{21}}+\omega_{01}\overrightarrow{I_{01}I_{21}})$

Dado que los dos vectores que se multiplican no pueden ser paralelos esto implica que

$\omega_{20}\overrightarrow{I_{20}I_{21}}+\omega_{01}\overrightarrow{I_{01}I_{21}}=\vec{0}\qquad\Rightarrow\qquad\overrightarrow{I_{20}I_{21}}=-\frac{\omega_{01}}{\omega_{20}}\overrightarrow{I_{01}I_{21}}$

Por tanto, puesto que el vector que une

I 21

con

I 20

es proporcional al que lo une con

I 01

, los tres puntos están alineados.

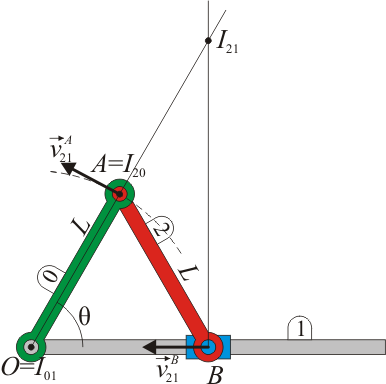
Así, por ejemplo, en el sistema biela-manivela, el CIR

I 01

es el punto O, alrededor del cual gira la manivela. El CIR

I 20

es A, la articulación entre la biela y la manivela. El CIR

I 21

se encuentra en la intersección de la recta que pasa por B y es perpendicular a $\vec{v}^B_{21}$ , con la recta que pasa por A y es perpendicular a $\vec{v}^A_{21}$ , pero esta última recta perpendicular es justamente la que pasa por O y A, que son los otros dos centros de rotación, por lo que los tres están alineados.

Este resultado es generalizable al caso de que alguno de los movimientos sea una traslación. Supongamos que el movimiento de arrastre {01} es una traslación con velocidad de traslación $\vec{v}^P_{01}=\vec{v}_0$ . En ese caso tenemos

$\vec{0}=\vec{v}^{I_{21}}_{21}=\vec{v}^{I_{21}}_{20}+\vec{v}^{I_{21}}_{01}$

Sustituyendo las velocidades relativa y de arrastre

$\vec{0}=\omega_{20}\vec{k}\times\overrightarrow{I_{20}I_{21}}+\vec{v}_0$

Proyectando y despejando

$\overrightarrow{I_{20}I_{21}}=\frac{\vec{k}\times\vec{v}_0}{\omega_{20}}$

Por tanto, la línea que une los centros

I 20

I 21

es perpendicular a la velocidad de traslación $\vec{v}_0$ , en cuyo “extremo” se encuentra el CIR

I 01

(que, por ser una traslación, es un punto del infinito).

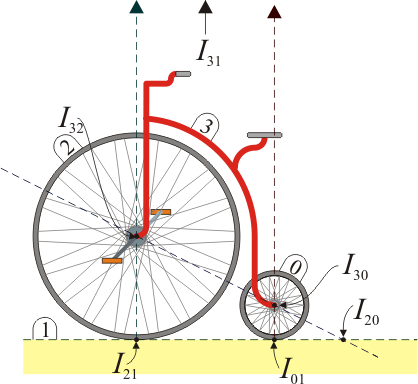
Como ilustración consideremos el caso de un carro “3” cuya rueda “2” se encuentra rodando sobre el suelo horizontal “1”. En este caso el CIR {32} es el centro de la rueda, mientras que el {21} es el punto de contacto de ésta con el suelo. El movimiento {31} es uno de traslación horizontal, por lo que su CIR

I 31

se encuentra en el infinito en una dirección vertical. Dado que el centro de la rueda y el punto de apoyo se encuentran sobre la misma vertical, los tres centros están alineados.

El teorema de los tres centros permite determinar gráficamente la posición de los centros instantáneos de rotación de sistemas de más de tres sólidos, a partir del conocimiento de algunos de ellos. Consideremos, por ejemplo, el velocípedo de la figura. En esta figura aparecen cuatro sólidos destacados:

Sólido 0: La rueda trasera
Sólido 1: El suelo
Sólido 2: La rueda delantera
Sólido 3: El cuadro del velocípedo

Las dos ruedas realizan, respecto del cuadro “3”, movimientos de rotación alrededor de sus respectivos ejes. Por ello, el CIR

I 32

es el centro de la rueda delantera “2” y el CIR

I 30

el de la trasera “0”.

Respecto del suelo “1” cada rueda efectúa una rotación instantánea alrededor del punto de contacto. Por ello, el punto de apoyo de la rueda delantera es el CIR

I 21

y el de la trasera es el

I 01

Nos preguntamos entonces por la posición del CIR

I 20

, esto es, desde un sistema solidario con la rueda trasera, ¿alrededor de que punto gira la delantera? Por el teorema de los tres centros,

I 20

se encuentra alineado con

I 21

y con

I 01

. Por tanto, debe encontrarse sobre la línea horizontal del suelo. Por el mismo teorema,

I 20

debe estar alineado con

I 32

y con

I 30

, lo que supone que debe hallarse en la recta que une los centros de las dos ruedas. Por ello, debe encontrarse en la intersección de esta recta con la horizontal del suelo. El resultado es un punto que no pertenece al sólido real “0” ni al “2”, sino que se encuentra a una cierta distancia por detrás del vehículo.

Podemos preguntarnos también por la ubicación del CIR

I 31

, correspondiente al movimiento del cuadro respecto al suelo. Este CIR se encuentra alineado, por un lado con los centros

I 30

I 01

, y por otro con los centros

I 32

I 21

. Estas dos rectas, sin embargo, son paralelas, ya que ambos pares de puntos se encuentran sobre sendas verticales. El CIR

I 31

se encuentra por tanto en el infinito, sobre una dirección perpendicular a la horizontal. Esto corresponde a que el cuadro realiza un movimiento de traslación cuya velocidad es horizontal, indicando el avance del velocípedo.

atp2014-13

jaj

jaj

jaj

jaj

jaj

sábado, 11 de octubre de 2014

Tridimensional

Índice

Espacio físico tridimensional[editar]

Ejemplos de formas tridimensionales[editar]

Sistemas tridimensionales en ciencias naturales[editar]

Simulación 3D[editar]

Véase

Tridimensional

Índice

Espacio físico tridimensional[editar]

Ejemplos de formas tridimensionales[editar]

Sistemas tridimensionales en ciencias naturales[editar]

Simulación 3D[editar]

Véase

homotecia

simetría central

simetria axial

Simetría axial

Definición de movimiento plano

2 Propiedades del movimiento plano

3 Centro instantáneo de rotación (C.I.R.)

3.1 Definición

3.2 Propiedades

3.3 Determinación del CIR

3.3.1 Procedimiento analítico

3.3.2 Procedimiento geométrico o gráfico

4 Composición de movimientos planos

4.1 Teorema de los tres centros